3. Confusion matrix(오차행렬) 와 정밀도, 재현율, F1 score

이진 분류 (0 , 1 두 가지로 분류) 상황에서
Positive / Nagative 는 예측값이 1(Positive) / 0 (Nagative) 임을 의미하고,
True / False 는 예측값이 진짜로 맞았는지 틀렸는지를 의미한다.
TP(True Positive) 는 모델이 참으로 예측했고, 실제로도(답이) 참이었던 경우
FP 는 참으로 예측했으나, 답은 거짓이었던 경우를 말한다.
가령 특정 데이터를 바탕으로 췌장암 예측모델을 만들었으며, 암 유/무 를 1과 0으로 표현할 떄
췌장암 환자라고 예측 -> 진짜로 췌장암 환자였다 : TP
췌장암 환자가 아니라고 예측 -> 사실 췌장암 환자였다 : FN 로 표현한다.
그리고 TP, TN, FP, FN 네 가지를 표현한 매트릭스를 Confusion Matrix, 오차행렬이라 한다.
ML 모델의 성능을 평가하는 지표 중에는 정확도, 정밀도, 재현율 등등이 있다.
정확도
Accuracy = (TP + TN) / (TP + TN + FP + FN)
(전체 중 예측에 성공한 비율)
정밀도
Precisions (Positive Predictive Value, PPV) = TP / TP + FP
(Positive 로 예측한 것중 예측에 성공한 비율)
재현율
Recall (Sensitivity, True Positive Rate, TPR) = TP / TP + FN
(정답이 Positive 인 것 중에 예측에 성공한 비율)
정확도, 정밀도, 재현율에는 허점이 존재한다.
독감이 대유행해서 100중 1명 꼴로 독감에 걸렸다고 하자.
그리고 독감에 걸렸는지 유무를 예측하는 모델을 만들었는데,
이 모델은 그냥 보는 사람 족족 독감에 걸리지 않았다고 예측한다.
그렇다면 100 명중에 99명은 예측에 성공한 셈이므로 정확도 99% 의 모델이 된다.
정밀도는 99 / (99 + 1)
재현율은 99 / (99 + 0)
예측모델이라기 보다 찍기모델에 가깝지만,
Positive 가 극히 적은 데이터셋에서 무조건 Nagative 라 예측하기만 해도
TP : 높음, FP: 낮음, TN: 0, FN: 0 이므로 정확도, 정밀도, 재현율 모두 높게 나온다.
반대로 Nagative 가 극히 적은 데이터셋에서 무조건 Positive 라 예측한 경우도 마찬가지이다.
정밀도 - 재현율 트레이드오프 (Trade-off)
Precisions (Positive Predictive Value, PPV) = TP / TP + FP
Recall (Sensitivity, True Positive Rate, TPR) = TP / TP + FN
TP는 둘의 공통인수니까 배제하고,
정밀도의 경우 FP 가 낮다면 높은 정밀도 수치, FN 가 낮다면 높은 재현율 수치를 얻을 수 있다.
가령 Postive 라고 예측하는 기준이 후하다면 어떨까?, 반대로 말하면 Nagative 라고 예측하는 기준은 빡빡해지는 셈이다.
Positive 라고 잘못 예측한, FP 값은 증가하고 Nagative 라고 잘못예측한 FN 값은 감소한다.
즉, FP 와 FN 은 반대방향의 추세를 가지는 값이다. 한 쪽이 증가하면 다른 한 쪽은 감소한다.
고로 FP 가 낮다면 정밀도는 높겠지만, FN 이 크기 때문에 재현율이 떨어지고
반대로 FP 가 높다면 정밀도는 떨어지지만 FN 이 낮기 때문에 재현율은 높아진다.
예측 모델의 목적에 따라 정밀도와 재현율 중 어떤 것이 더 중요한 평가지표인지가 달라진다.
예를 들어, 간암 환자 여부를 예측하는 경우는 정밀도보다 재현율이 더 중요하다.
참이라고 잘못 예측(FP)해도 상관없지만 (낮은 정밀도), 참이라는 정답을 거의 반드시 맞춰야 하는 경우 (높은 재현율) 에 해당한다.
간암환자가 아닌데 간암환자로 오진한 경우는 사실 별 상관없지만,
간암환자인데 간암환자가 아니라고 오진한 경우는 생사가 오가는 문제이기 때문이다.
반대로
SF 적인 예시이긴 하지만, 영화 마이너리티 리포트처럼 미래에 강력범죄를 저지르는 사람을 예측하는 모델이 있다고 치자.
예비 범죄자다 (Positive) / 아니다 (Nagative) 로 구분할 때,
범죄자가 아닌데 범죄자로 오진하는 경우 (FP) 가 범죄자인데 범죄자가 아니라고 오진하는 경우 (FN) 보다 훨씬 중요하다.
따라서 참이라고 잘못 예측(FP) 하면 큰일나지만, 참이라는 정답을 못맞추는 일은 비교적 덜 중요한 (FN) 경우에 해당한다
FP 가 낮은 게, FN 가 낳은 경우보다 더 중요하므로 바꿔말하면 정확도가 정밀도보다 중요한 경우이다.
정리하자면,
정밀도가 높을수록 재현율은 낮아지고
반대로 정밀도가 낮을수록 재현율이 높아지므로 목적에 맞게 정밀도가 높은 모델을 쓰거나, 재현율이 높은 모델을 쓴다.
그리고 정밀도를 높일려면 (재현율은 낮아지겠지만) FP 를 낮추기 위해
-> Positive 라고 예측하는 기준을 엄격하게 하면 된다.
-> (동치) Nagative 라고 예측하는 기준을 널널하게 한다.
반대로 재현율을 높일려면 (정밀도는 낮아지겠지만) FN 를 낮추기 위해
-> Nagative 라고 예측하는 기준을 엄격하게 하면 된다.
-> (동치) Positive 라고 예측하는 기준을 널널하게 한다.
편하게 "기준을 엄격하게 (널널하게 ) " 한다고 표현했으나,
임계치를 조정한다고도 이야기 한다.

데이터 값이 임계치(Threshold 라 한다)이상이면 P
아니라면 N라고 이진 분류한다고 하자.
Threshold 값을 높이면, P 로 분류되는 개수가 적어지고,
반대로 낮추면 P 로 분류되는 개수가 많아진다.
오차행렬과 정밀도, 재현율
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score, precision_score, recall_score, confusion_matrix
from sklearn.linear_model import LogisticRegression
import pandas as pd
import numpy as np
def get_clf_eval(y_test, pred):
confusion = confusion_matrix(y_test, pred)
accuracy = accuracy_score(y_test, pred)
precision = precision_score(y_test, pred)
recall = recall_score(y_test, pred)
print("오차 행렬")
print(confusion)
print("정확도 = {0}, 정밀도 = {1}, 재현율 = {2}".format(np.round(accuracy, 4), np.round(precision, 4), np.round(recall, 4)))
return [confusion, accuracy, precision, recall]여기까지가 accuracy_score, precisio_score, recall_score 메서드의 사용법이고
파라미터 y_test 는 데이터셋들의 예측에 대한 정답, pred 는 생성한 모델이 예측한 값이다.
둘 다 np.ndarray 타입이며 즉, N x 1 테이블 형태이다.
말로만 하면 애매하니 밑에 나머지 코드 전체를 가져왔다.
titanic_df = pd.read_csv('./titanic_train.csv')
titanic_df.head()
titanic_x_df = titanic_df.drop("Survived", axis=1)
titanic_y_df = titanic_df['Survived']
from sklearn.preprocessing import LabelEncoder
# 결측값 (NaN) 처리
def fillna(df):
df['Age'].fillna(df['Age'].mean(), inplace=True)
df['Cabin'].fillna('N', inplace=True)
df['Embarked'].fillna('N', inplace=True)
df['Fare'].fillna(0, inplace=True)
return df
# ML 에 불필요한 피처 제거
def drop_features(df):
df.drop(['PassengerId', 'Name', 'Ticket'], axis=1, inplace=True)
return df
# string type 데이터 인코딩 (int) == 레이블 인코딩
def format_features(df):
df['Cabin'] = df['Cabin'].str[:1]
features = ['Cabin', 'Sex', 'Embarked']
le = LabelEncoder()
for feature in features:
le.fit(df[feature])
df[feature] = le.transform(df[feature])
return df
def transform_features(df):
fillna(df)
drop_features(df)
format_features(df)
return df
titanic_x_df = transform_features(titanic_x_df)
x_train, x_test, y_train, y_test = train_test_split(titanic_x_df, titanic_y_df, test_size = 0.2, random_state=11)
lr_clf = LogisticRegression(solver='liblinear') # solver(알고리즘) 기본값은 lbfgs, 소규모 데이터셋의 경우 통상 liblinear 가 약간 더 나음
lr_clf.fit(x_train, y_train)
pred = lr_clf.predict(x_test)
clf_eval = []
clf_eval.append(get_clf_eval(y_test, pred))Sckit-Learn 에서 Threshold 값의 변화에 따른 정확도 - 재현율 트레이드 오프 시각화
from sklearn.preprocessing import Binarizer
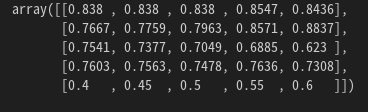
arr = np.round(np.random.rand(3,2), 2)
binarizer = Binarizer(threshold=0.3).fit(arr)
pred_arr = binarizer.transform(arr)
print(arr)
print(pred_arr)
Binarizer 로 배열의 원소값이 threshold 값 이상이라면 1, 아니라면 0의 값으로 변환할 수 있다.
x_train, x_test, y_train, y_test = train_test_split(titanic_x_df, titanic_y_df, test_size = 0.2, random_state=11)
# solver(알고리즘) 기본값은 lbfgs, 소규모 데이터셋의 경우 통상 liblinear 가 약간 더 나음
lr_clf = LogisticRegression(solver='liblinear')
lr_clf.fit(x_train, y_train)
pred = lr_clf.predict(x_test)
clf_eval = []
clf_eval.append(get_clf_eval(y_test, pred))
pred_proba = lr_clf.predict_proba(x_test)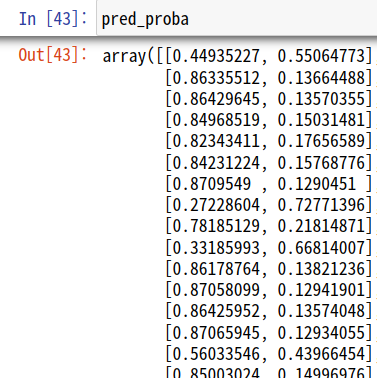
Logistic regression classifier 객체의
predict_proba 메서드는 데이터가 0(Nagative)일 확률, 1(Positive)일 확률을 행으로 하는 테이블을 반환한다.
import matplotlib.pyplot as plt
def precision_recall_curve_plot(y_test, pred_proba):
precisions, recalls, thresholds = precision_recall_curve(y_test, pred_proba)
thr_count = thresholds.shape[0]
plt.plot(thresholds, precisions[:thr_count], label='precision')
plt.plot(thresholds, recalls[:thr_count], label='recall')
# x 축 범위와 간격
start, end = plt.xlim()
plt.xticks(np.round(np.arange(start, end, 0.1), 2))
plt.xlabel('Thresholds')
plt.legend()
plt.show()
precision_recall_curve_plot(y_test, pred_proba_1)
정확도와 재현율은 Threshold 값의 증가 대해 서로 상반된 변화 추세를 보여줌을 시각화 하여 볼 수 있다.
F1 score
정밀도와 재현율을 결합한 지표
F1 Score = 2 * (precision * recall) / (precision + recall)
1행부터 순서대로, 정확도, 정밀도, 재현율, f1 점수, threshold 값이다.